Mathematics of Enhanced Portfolio Returns

In the financial world, Harry Markowitz's Modern Portfolio Theory has long been regarded as the gold standard for optimizing investment portfolios. MPT’s core principle—that diversification across assets with low correlations can yield higher returns with reduced overall risk—remains foundational. By strategically allocating assets such as real estate, private equity, and hedge funds, which demonstrate disparate correlations to traditional stocks and bonds, institutional investors have historically pursued the elusive balance of maximizing returns while minimizing risk. However, while MPT provides a robust framework, emerging theories suggest that further enhancing portfolio performance might be possible through more nuanced and mathematical approaches.

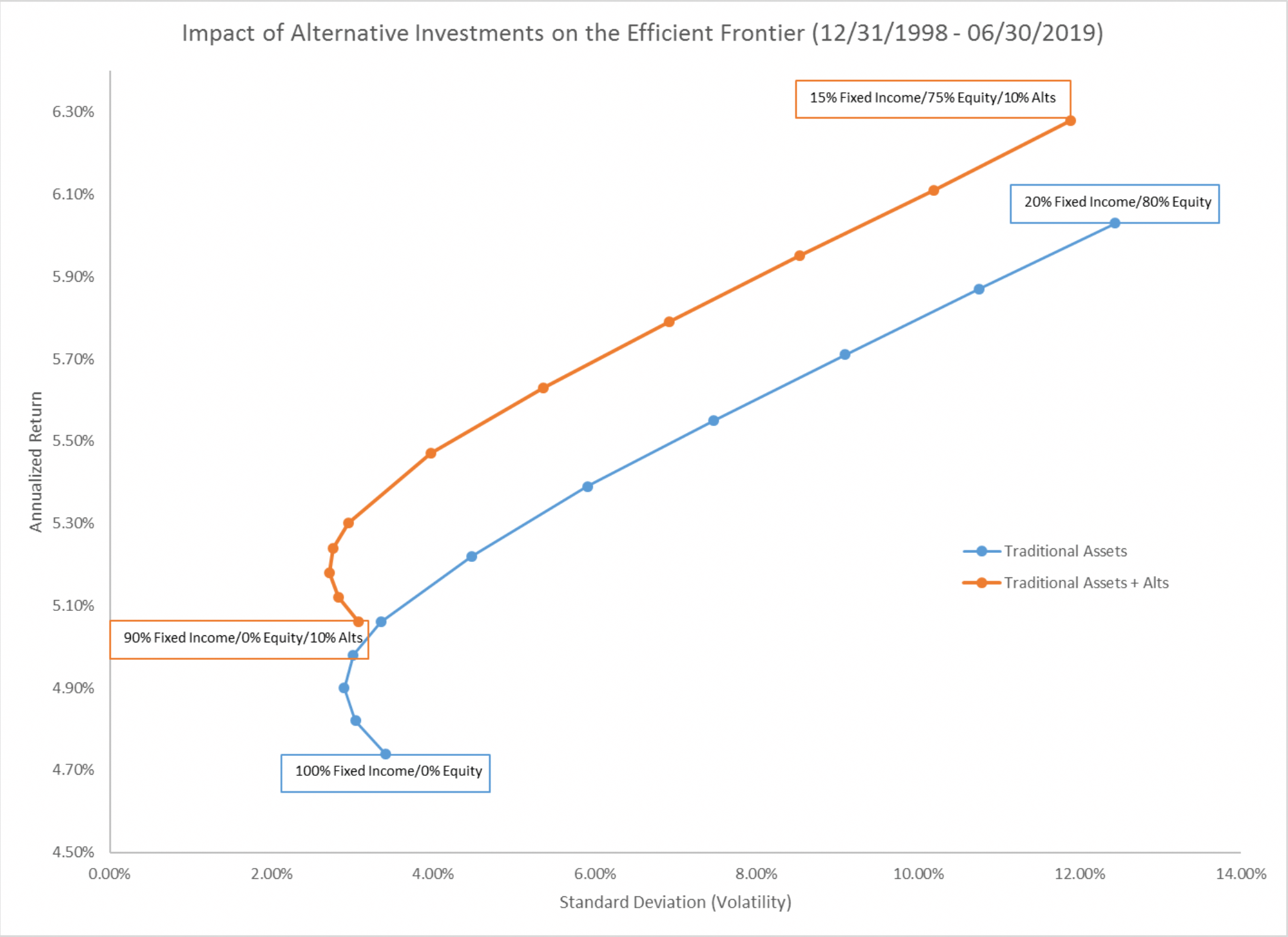
Shannon’s Demon Concept in Portfolio Management

An intriguing yet less known concept "Shannon's Demon" may offer a critical tool for investors aiming to increase returns and reduce risks over time. Named after Claude Shannon, the father of information theory, this concept extends beyond traditional finance to introduce a counterintuitive but mathematically sound strategy. Shannon’s Demon posits that a portfolio comprising two uncorrelated assets, each with zero or negative expected returns, can still generate positive returns at the portfolio level through systematic rebalancing. This finding challenges conventional wisdom and provides a unique perspective on portfolio optimization, demonstrating that sophisticated mathematical insights can pre-determine long term wealth generation.

From Coin Flips to Consistent Returns

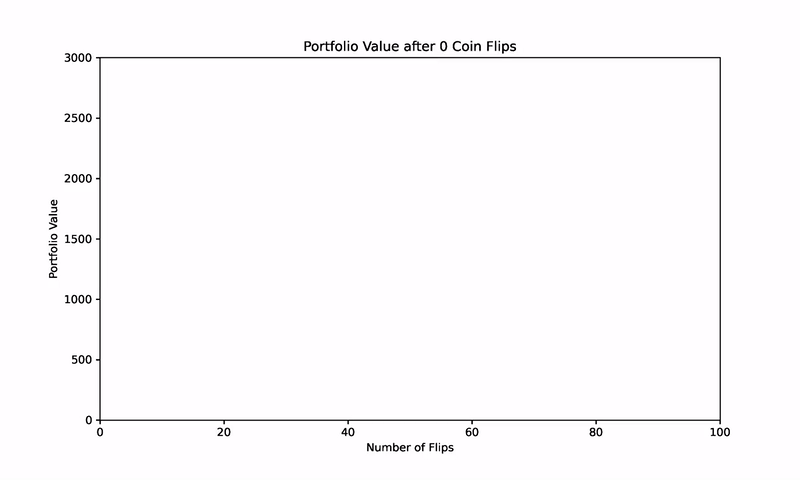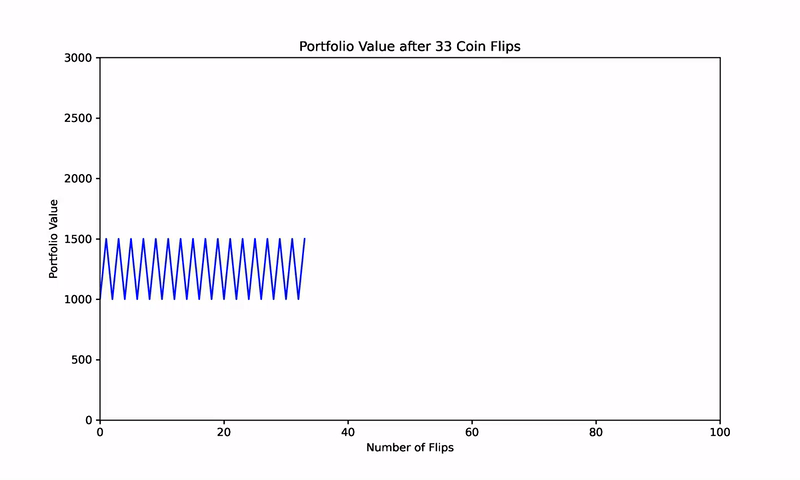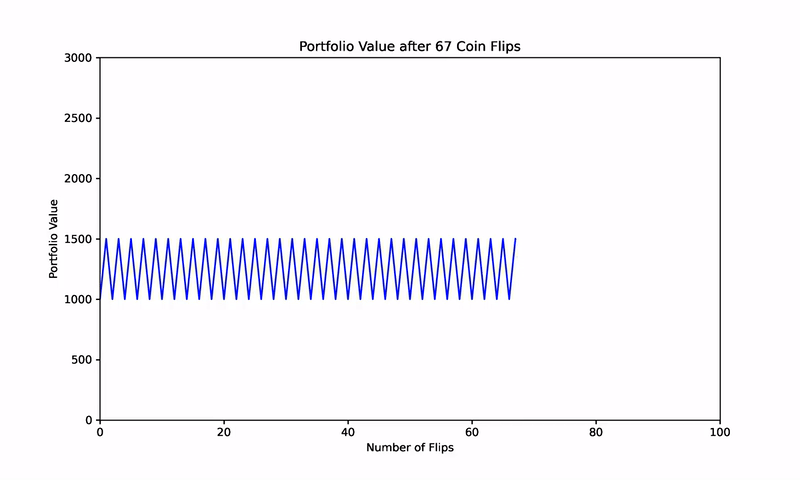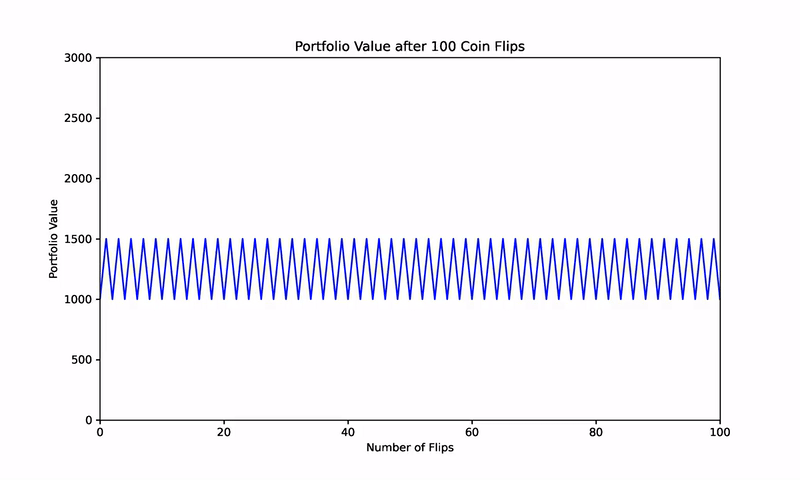
To understand the power of Shannon’s Demon, consider a simplified example involving a coin-flip game. In this game, a coin flip yields a 50% gain if it lands on heads but results in a 33.3% loss if it lands on tails. Over time, the expected return from this game is zero, as wins and losses statistically cancel each other out.

For instance, starting with $100, an initial heads outcome might boost the value to $150, while a subsequent tails outcome would reduce it back to $100. Without intervention, the portfolio would oscillate around this initial value, generating no long-term gains.

However, the magic of Shannon’s Demon emerges when we introduce a systematic rebalancing strategy. Suppose, after each coin flip, you rebalance the portfolio to maintain a 50% allocation to the game and the remaining 50% in cash. Despite the zero expected returns from both the coin game and cash, this rebalancing strategy transforms the portfolio’s performance.

For example, starting with $100, $50 is allocated to the game, and $50 is held in cash. A win (heads) increases the portfolio to $125, which is then rebalanced to $62.5 in the game and $62.5 in cash. A loss (tails) reduces the portfolio value, but rebalancing after each flip creates a mechanism for gradual growth.

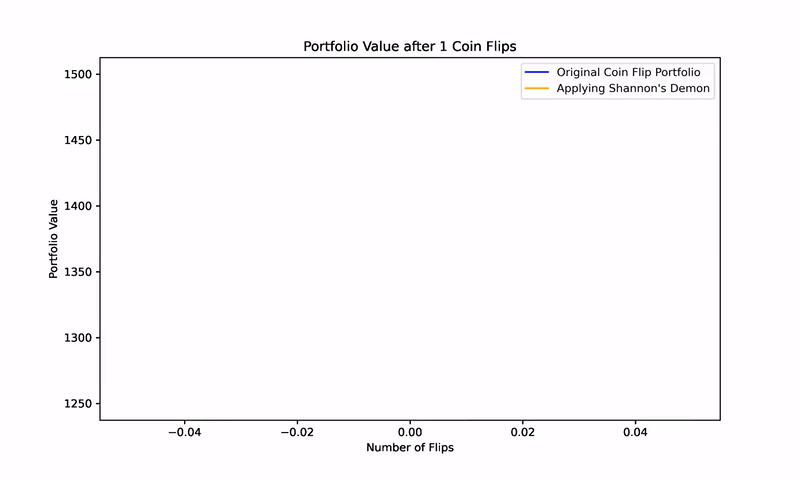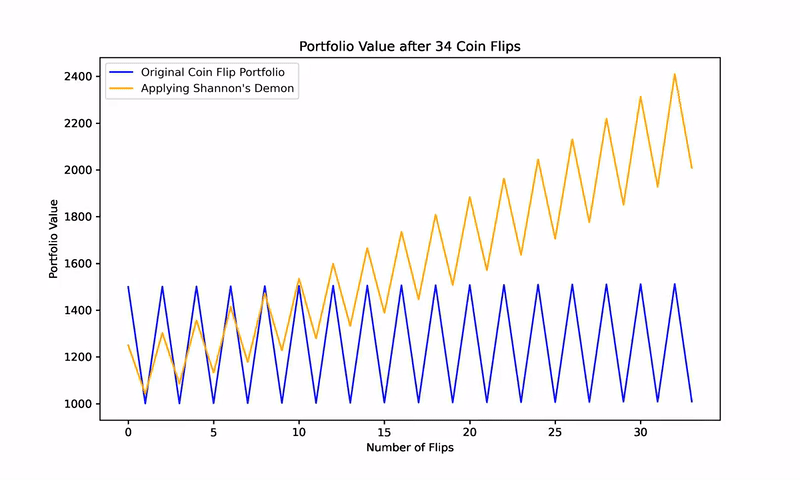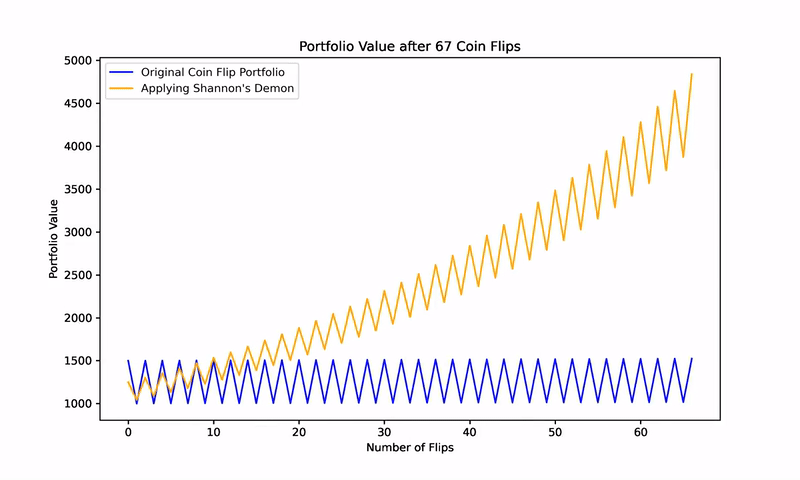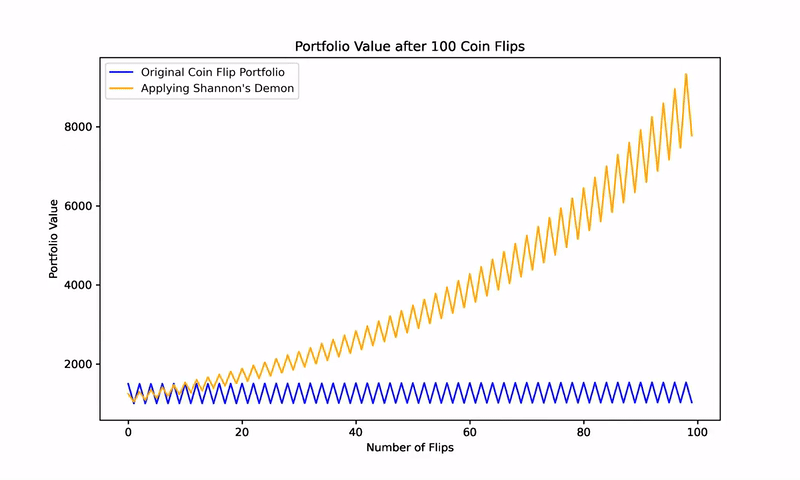
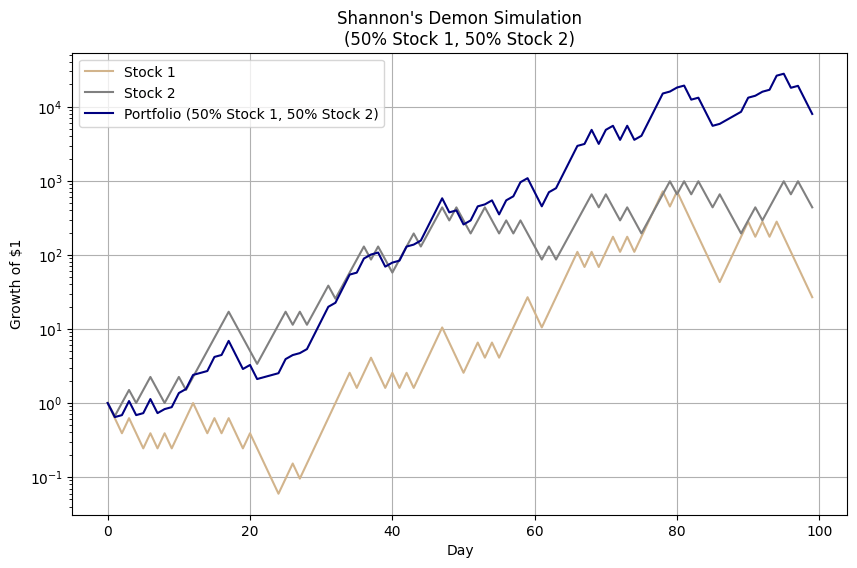
Simulating Shannon’s Demon

To further validate this concept, consider a simulation of 1,000 randomized coin flips. Without rebalancing, the results cluster around a zero net return, aligning with the expected outcome of the game.

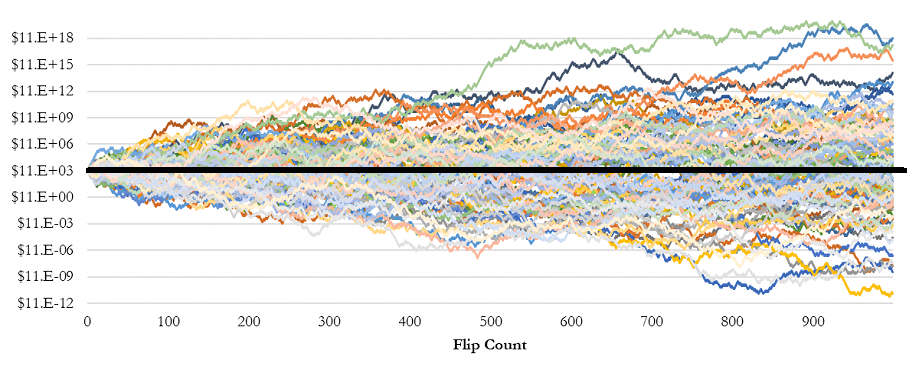
However, when a 50% rebalancing strategy is applied after each flip, the portfolio begins to consistently generate positive returns. This counterintuitive result, depicted in subsequent figures, illustrates how two assets with zero expected returns can, through rebalancing, become a wealth-generating portfolio.

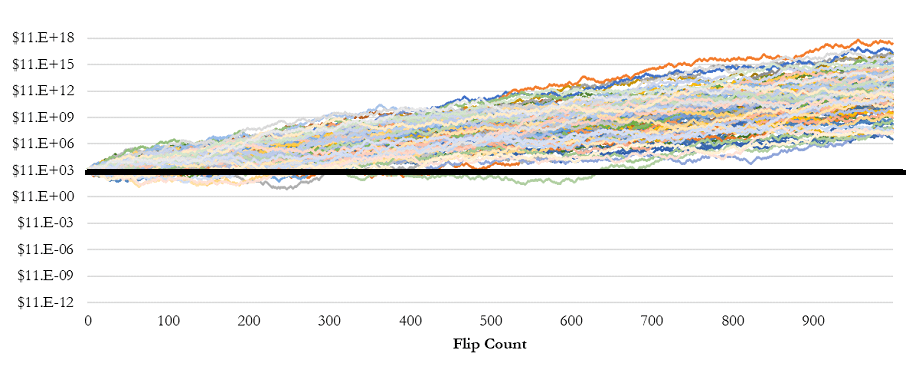
The Mechanism Behind Shannon’s Demon: Understanding Volatility Drag

The success of Shannon’s Demon hinges on mitigating a phenomenon known as "volatility drag." This concept is pivotal in understanding how rebalancing can turn two zero-return assets into a profitable portfolio. Volatility drag occurs when the variability in returns negatively impacts the overall performance of an investment.

To illustrate, consider an investment of $100. In the first year, a 10% gain increases the value to $110, but a subsequent 10% loss reduces it to $99, leaving the investor down by 1%. The impact of volatility becomes even more pronounced with larger fluctuations. For instance, with a 20% gain followed by a 20% loss, the final value drops to $96—a 4% loss. This exponential increase in volatility drag means that as volatility doubles, the loss quadruples, severely hampering the investment’s growth.

The implications are significant: even if the average return is positive, high volatility can erode these gains, potentially driving the return to zero. In mathematical terms, if the average return is greater than zero but less than half the variance (SD²/2), rebalancing becomes crucial. Through this strategy, an investor can construct an optimal portfolio that maximizes long-term Compound Annual Growth Rate (CAGR) by reducing volatility drag.

Volatility Drag and Portfolio Returns

Shannon’s Demon demonstrates that reducing volatility drag through rebalancing can transform the arithmetic average return into a more meaningful geometric average return, which reflects the actual growth of the portfolio over time. Shannon suggested dividing investment capital equally between a volatile stock and cash, then rebalancing daily to maintain this 50/50 allocation. In this scenario, the stock experiences extreme volatility, either doubling or halving in value daily.

A buy-and-hold investor who fully commits to the stock would see no net gain over time. Conversely, the investor who follows Shannon’s strategy, continuously rebalancing with cash, ends up with a profitable portfolio. Although this example involves unrealistic volatility (a theoretical 25% average return with a 75% standard deviation), it underscores a key point: rebalancing can convert a zero-return scenario into a positive outcome by mitigating volatility drag.

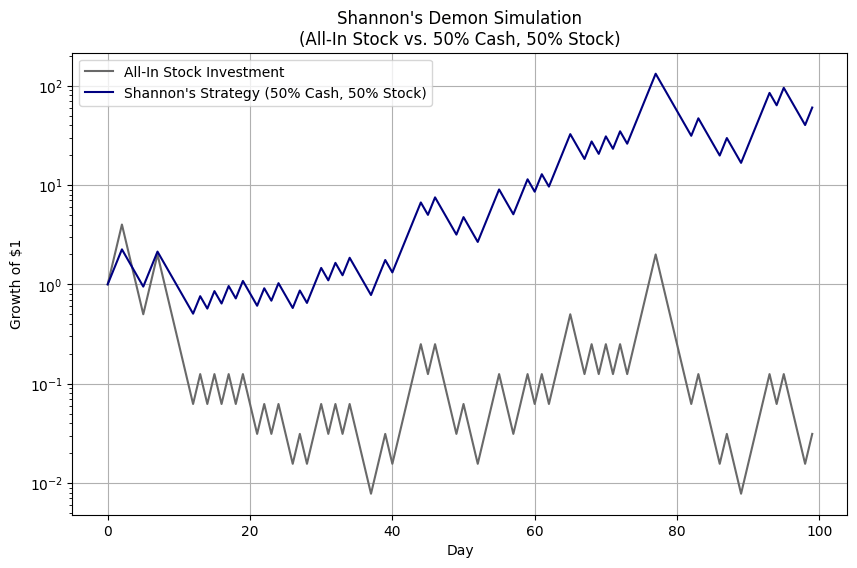
In practical terms, the arithmetic average expected return in our coin-flip game was approximately 8.4%. However, due to volatility drag, the expected geometric return was zero. This discrepancy—where the expected return seemingly vanishes—is explained by the following formula:

Arithmetic Average Return – Volatility Drag ≈ Geometric Average Return

Where volatility drag is approximately equal to half the variance (Volatility²/2). Applying this to our coin-flip game:

8.4% - (42%² ÷ 2) ≈ 0%

As volatility increases, the drag on returns grows exponentially. By rebalancing and thus reducing overall portfolio volatility, an investor can decrease the volatility drag more than the reduction in the arithmetic return, effectively turning a 0% expected geometric return into a positive one.

In our coin-flip example, rebalancing 50% into cash after each flip reduces the arithmetic return by half, but it also cuts volatility drag by 75%, resulting in a positive expected geometric return of approximately 2%.

4.2% - (21%² ÷ 2) ≈ 2%

Practical Implications

The power of rebalancing extends beyond theoretical constructs. Even in real-world portfolios, reducing volatility drag through diversification and systematic rebalancing can significantly enhance returns. For example, a 50/50 portfolio of the Vanguard 500 Index Fund and Vanguard Long-Term Treasury, rebalanced annually, outperformed both individual assets from 1986 to 2010, achieving a CAGR of 9.17% with lower volatility. Similarly, a portfolio of stocks and gold, regularly rebalanced over four decades, yielded a higher return than either asset alone. These examples underscore that diversification and rebalancing can turn seemingly average investments into robust, wealth-generating portfolios.

Final Thoughts

While the coin-flip game is a theoretical construct, the principles underlying Shannon’s Demon have significant implications for real-world investing. By applying rebalancing strategies to assets with low or negative correlations, investors can potentially achieve higher returns without increasing risk. This approach requires more sophisticated modeling and a deeper understanding of market dynamics, but the underlying concept remains powerful.

In an environment where traditional high-yield investments often come with hidden risks, the concepts behind Shannon’s Demon offer a compelling alternative. By focusing on reducing volatility drag through diversification and rebalancing, investors can achieve attractive yields without chasing risky assets. While finding assets with positive expected returns is preferable, the principles of Shannon’s Demon show that even assets with zero or negative returns can contribute positively to a portfolio when managed correctly.

In conclusion, Shannon’s Demon is not just a theoretical exercise but a practical strategy that can help investors navigate today’s complex financial landscape, turning uncertainty into opportunity by strategically minimizing losses and maximizing long-term gains.